BESSEL (FONCTIONS DE)

BESSEL (FONCTIONS DE)

Les fonctions de Bessel jouent un rôle important en mathématiques appliquées et en physique mathématique. Elles interviennent aussi bien dans des problèmes de conduction de la chaleur que dans des problèmes de diffraction, acoustique, ou électromagnétisme. Elles apparaissent souvent dans l’étude d’équations différentielles ou d’équations aux dérivées partielles avec des conditions aux limites relatives à des frontières sphériques ou cylindriques. Ces fonctions possèdent certaines analogies avec les fonctions trigonométriques: comportement à l’infini, zéros, développement en série.

Définitions

Considérons l’équation différentielle:

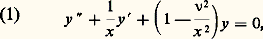dans laquelle 益 est un paramètre complexe quelconque. Les fonctions de Bessel, ainsi que d’autres fonctions voisines, les fonctions de Neumann et de Hankel, sont des solutions particulières de cette équation différentielle. Supposant que x est une variable réelle positive, cherchons des solutions de la forme:

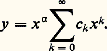Par identification terme à terme, on obtient:

donc, on doit avoir 見 = 梁 益.

Si on choisit 見 = 益, on trouve:

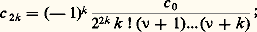on est alors amené à choisir:

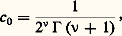d’où: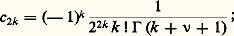

臨 désigne ici la fonction eulérienne; c’est une fonction continue qui a pour propriété fondamentale 臨(n + 1) = n ! pour n entier (cf. fonction GAMMA).

Par définition, la fonction de Bessel J size=1^益, d’indice 益, est donnée par ces coefficients, soit:

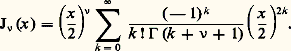La série qui intervient dans la définition de J size=1^益 converge pour tout x réel et on vérifie que J size=1^益 satisfait à l’équation différentielle donnée. Si 益 est entier, J size=1^益 peut être définie pour tout x complexe. Si 益 n’est pas entier, on peut étendre le domaine de définition de J size=1^益 à l’ensemble des x complexes non nuls, mais l’origine sera un point critique à cause du facteur (x /2) size=1^益.

Si 益 n’est pas entier, la solution 見 = 漣 益 fournit la fonction:

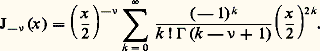J size=1^漣 size=1^益 est encore une solution de l’équation différentielle (1), et on vérifie que J size=1^漣 size=1^益 et J size=1^益 sont linéairement indépendantes. La solution générale de (1) est donc:

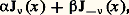見 et 廓 étant deux constantes arbitraires. Si 益 est un entier n , on constate que:

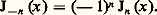Tous ces faits peuvent être justifiés en remarquant que l’équation différentielle (1) est une équation du type de Fuchs (cf. équations DIFFÉRENTIELLES), dont l’équation déterminante est x ² + 益² = 0. La différence des racines de l’équation déterminante est 2 益. Si 2 益 n’est pas entier, on a une base de la forme x 益 A(x ) et x 漣 益 B(x ), A(x ) et B(x ) étant deux fonctions holomorphes au voisinage de x = 0. Si 2 益 est entier, on n’obtient ainsi qu’une seule solution x 益 A(x ). Pour obtenir une deuxième solution dans ce cas, on est amené à introduire les fonctions de Neumann. Pour 益 non entier, on appelle fonction de Neumann d’indice 益, N size=1^益, la fonction:

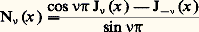pour 益 non entier et:

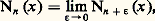pour n entier. On vérifie alors que, pour tout 益, la fonction de Neumann est une solution de (1) et que Nⁿ et Jⁿ sont linéairement indépendantes. Donc, si n est entier, la solution générale de (1) est:

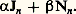Enfin, on introduit parfois les fonctions de Hankel:

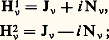que 益 soit entier ou non, H size=1^益1 et H size=1^益2 forment une base de solutions de (1).

Propriétés principales

Formules asymptotiques. Le comportement à l’infini des fonctions introduites est donné par les formules:

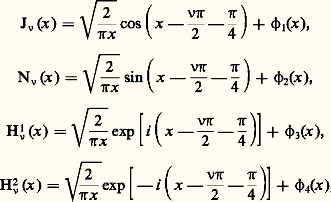où les fonctions 﨏ⁱ (x ) tendent vers zéro lorsque x tend vers l’infini avec |arg x | 諒 神 漣 﨎, 﨎 礪0; d’une manière plus précise, les quantités x ^3/2 﨏ⁱ (x ) restent bornées.

Formules de récurrence. À partir des développements en séries, on obtient les deux formules de récurrence:

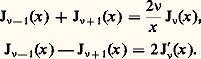Voici une application de ces formules.

On vérifie directement que:

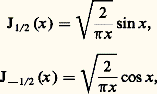par suite, si 益 est de la forme n + 1/2, avec n entier, les formules de récurrence montrent que J size=1^益 est une combinaison linéaire de fonctions élémentaires.

Représentation intégrale. Il est souvent commode de représenter J size=1^益 sous la forme d’une intégrale. On a la formule:

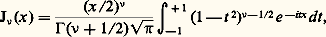qui est valable pour Re 益 + 1/2 礪0.

Fonction génératrice. Les fonctions de Bessel sont liées à un développement en série de Laurent. En effet, introduisons la fonction:

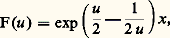pour u complexe et x paramètre complexe non nul; son développement en série de Laurent à l’origine s’écrit:

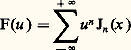(formule de Schlömilch). La fonction F(u ) est appelée fonction génératrice. Changeant u en 1/u et faisant le produit membre à membre des égalités obtenues, on obtient:

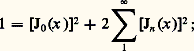on en déduit, pour tout x réel, les majorations: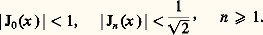

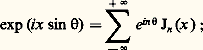Voici une autre présentation de la formule de Schlömilch; posant u = e ⁱ , on obtient:

les Jⁿ (x ) sont donc ainsi les coefficients de Fourier de la fonction:

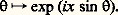Théorème de Neumann. À partir des fonctions de Bessel on peut obtenir des représentations analogues au développement en séries entières. Plus précisément, toute fonction holomorphe dans le disque |z | 麗R peut être développée en série sous la forme:

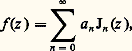où la série converge absolument et uniformément dans tout disque compact |z | 諒R¹ 麗R.

De plus, il faut signaler que l’on peut faire une théorie analogue à la transformation de Fourier en employant les fonctions de Bessel: soit f (x ) une fonction définie pour x 閭 0, à valeurs réelles ou complexes, continue par morceaux, telle que:

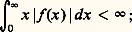pour tout entier n , positif, posons:

alors, on a la formule suivante d’inversion: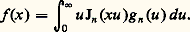

Des fonctions voisines des fonctions de Bessel sont parfois utilisées. Ce sont, par exemple:

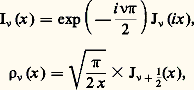appelées respectivement fonctions de Bessel modifiées, et fonctions de Bessel sphériques.

Encyclopédie Universelle. 2012.